[고등 확률과 통계] 2. 이항정리

확률과 통계 두번째 시간!

이항정리입니다.

 

이항정리는

이(二)! 두개의 항(項)! 항으로 이루어진 식을 거듭제곱한 것을 정리하는 겁니다.

 

곱셈공식으로도 충분히 확인할 수 있지만,

다음과 같이 생각해봅시다.

 

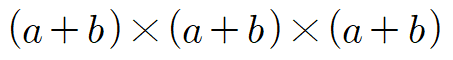
세 군데의 (a+b)에서 a를 한개씩 뽑아서 곱한다면 a³이 됩니다.

세 군데의 (a+b)에서 a 1개와 b 2개를 뽑아서 곱한다면 b³이 되는데,

3군데에서 a를 1개 뽑는 방법은 ₃C₁로 3가지입니다.

이를 식으로 표현하면 다음과 같습니다.

---

이렇게 만들어진 것이 파스칼의 삼각형입니다.

파스칼의 삼각형에는 여러 가지 규칙이 있습니다.

 

1) 삼각형 공식: 1+1=2

2) 하키스틱 공식: 1+3+6=10, 1+4=5

3) 가로 합: 1+3+3+1=8

4) 가로 좌측 절반 합 = 가로 우측 절반 합 (단, 항의 개수가 짝수 일 때)

5) 홀수번째 항의 합 = 짝수번째 항의 합

공식은 중요하니까 꼭 암기하도록 합시다!

 

3) 4) 5)의 공식은 이항계수의 성질이라고 알려져 있습니다.

---

이항계수의 성질은 다음과 같습니다.

 

이항정리에서는 다양한 문제들이 출제되는데요.

시험볼 때, 문제를 풀기전에 파스칼의 삼각형을 5~6줄 정도 그려두면

문제가 한결 쉽게 풀립니다.

꼭 그려보세요!

 

확률과 통계의 대단원 4개 중 1단원이 마무리 되었습니다.

다음시간부터는 확률을 배웁니다.

수고하셨습니다!