
안녕하세요! 수학을 잘하고 싶은 윤영진입니다.
수학2라는 책을 배워봅시다!
1단원이 함수의 극한이네요.
수학책들도 다른 책들(소설, 수필 등)과 마찬가지로 나름의 스토리를 갖고 있습니다.
수학2도 스토리를 갖고 있는데요.
수학2는 함수와 그 그래프를 잘 다루고 싶은 마음을 담은 책이예요.
기본적인 함수의 개념과 그래프 그리는 방법 정도는 알고 있어야 합니다.
함숫값과 조금 다르게, 어딘가에 가까워지는 값을 찾아보는 극한!
함수의 극한과 함숫값이 같을 때 연속이 되는 것을 배우고,
연속함수 중 부드러운 곡선일 때 접선의 기울기를 찾아봅니다.
이게 바로 미분이고요,
미분의 개념을 배운 후 접선의 방정식이나 극대, 극소, 최대, 최소등을 알아봅니다.
도형에 활용도 해보고요.
미분가능한 함수를 알았으니 반대의 연산! 적분을 해봅니다.
적분은 크게 부정적분과 정적분이 있는데, 그 두 가지의 개념을 잡고,
도형, 속도, 가속도 등에서 활용을 해보면 책이 마무리 됩니다.
그럼 가장 먼저 시작해야 하는 함수의 극한을 살펴보겠습니다.
새로 등장하는 용어에는
수렴, 발산, 좌극한, 우극한 등이 있습니다.
용어 개념을 알아본 후에 극한의 성질을 이해하고,
1. 함수의 극한값을 계산할 수 있고
2. 미정계수를 결정할 수 있으며
3. 함수의 극한의 대소관계를 이용하여 극한값을 구할 줄 알면
함수의 극한을 제대로 이해한 것입니다.
극한이란 함수에서 x의 값이 어떤 수(=값)에 가까워 질 때, 함숫값이 어디에 가까워지는 지!
예를 들어 f(x)=3x라는 함수에서 x가 2에 가까워진다면 함숫값은 6에 가까워지겠죠.
이 때 주의할 점은 x가 2는 아니고, 함숫값도 6은 아니라는 겁니다. 그냥 가까워진다고요.
위의 예에서 함숫값이 6에 가까워지는데, 6을 극한값이라고 합니다.
기호로는 아래와 같이 씁니다.

읽을 줄 알아야겠죠?
리미트 x가 2로 갈 때, 3x는 6
다시 한 번!
극한은 '함수에서 x의 값이 a(어떤 수)에 가까워 질 때, f(x)가 가까워지는 값'입니다.
극한의 개념을 정확히 알아야 좌극한과 우극한을 이해할 수 있습니다.
함수의 극한에는 수렴과 발산이 있습니다.
수렴은 특정한 값에 가까워 지는 것이고
발산은 무한히 커지거나, 무한히 작아지거나, 커졌다 작아졌다를 반복하는 세가지가 있습니다.
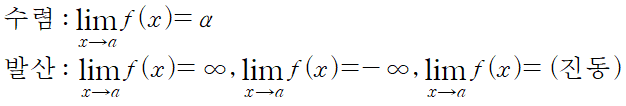
좌극한과 우극한을 알아보겠습니다.
좌극한은 극한값 중 x가 a보다 작은 쪽! 좌측에서 오고 있을 때의 극한값이고,
우극한은 극한값 중 x가 a보다 큰 쪽! 우측에서 오고 있을 때의 극한값입니다.

예를 들어 다음과 같은 분수함수가 있다고 합시다.
함수를 그려보세요. (그릴 줄 모른다면 과감히 포기하고, 중등과정부터 배웁시다!)

x가 0보다 작을 때, f(x)는 음수인데, x가 0에 가까워질수록 절댓값이 커지기 때문에 f(x)는 무한히 작아집니다.
x가 0보다 클 때, f(x)는 양수인데, x가 0에 가까워질수록 f(x)는 커집니다.

함수의 극한값은 좌극한과 우극한이 같을 때만 존재합니다!!!
함수의 극한은 다음 성질을 갖고 있습니다.
영어가 잔뜩 나와서 복잡해 보이지만,
간단히 설명하자면, 실수배, 덧셈, 뺄셈, 곱셈, 나눗셈, 이렇게 5가지가 가능하다는 이야기입니다.
물론 나눗셈에서 분모는 0이면 안됩니다.
그리고 이 5가지 성질은 극한값이 존재할 때만 성립합니다.

이제 함수의 극한값을 계산해보도록 하겠습니다.
극한값은 확정형과 부정형이 있는데요 (말만 어려워 보임.)
확정형은 그냥 딱 정해지는 겁니다.
예를 들어 분자는 수가 정해져 있는데, 분모가 무한히 커진다면 값은 한없이 작아져서 0에 가까워지겠죠.
다음과 같은 극한들은 확정형입니다.

부정형은 아직 정해지지 않은 것을 말하는데, 3가지가 있습니다. (시험 출제율 100%)
이 3가지는 반드시 알아두고 연습을 많이 해야합니다. (정말 중요해요.)

1)은 0분의 0꼴이라 합니다.
분자나 분모에 근호가 있다면 유리화를 먼저 합니다.
대부분의 문제는 '인수분해 → 약분 → 대입'해서 풀면 됩니다.


2)는 무한대분의 무한대꼴이라 합니다.
분자의 차수가 크다면 발산
분모의 차수가 크다면 0
차수가 같다면 '(분자의 최고차항의 계수)/(분모의 최고차항의 계수)'로 풀면 됩니다.

3)은 무한대 마이너스 무한대꼴이라 합니다.
보통은 근호가 포함된 경우가 많기 때문에 유리화만 해주면 쉽게 구할 수 있습니다.
근호가 없는 다항식인 경우는 최고차항으로 묶습니다.


극한값을 계산할 수 있다면,
이번에는 미정계수를 결정하는 문제를 풀어봅시다.

마지막으로 함수의 극한의 대소에 관계에 대한 문제를 풀 수 있다면 다 배웠습니다.
샌드위치정리를 사용해서 문제 푸는 건데, 이건 숙제라고 생각합시다.
각자 풀어보세요! 화이팅!
https://www.youtube.com/k5cOR0GM8c4
'수학 > 수학2' 카테고리의 다른 글
| [고2/고3 수학2] 6. 도함수의 활용(3) - 방정식, 부등식에의 활용, 속도, 가속도 (0) | 2021.07.21 |
|---|---|
| [고2/고3 수학2] 5. 도함수의 활용(2) - 증가, 감소, 극대, 극소 (0) | 2021.07.21 |
| [고2/고3 수학2] 4. 도함수의 활용(1) 접선의 방정식 (0) | 2021.07.15 |
| [고2/고3 수학2] 3. 미분계수와 도함수 (0) | 2021.07.15 |
| [고2/고3 수학2] 2. 함수의 연속 (0) | 2021.07.15 |




댓글