
드디어 수학의 꽃! 미적분! 그 중에서도 미분을 배웁니다.
수학의 꽃이라는 표현을 쓰는 이유는
아마도 중, 고등과정에서 배운 방정식, 부등식, 함수, 점과 좌표들이 최종적으로 결실을 맺는 단원이기 때문일 것입니다.
제가 설명하는 것은 고등학교 과정의 입시(수능, 내신)를 위한 미적분일 뿐입니다.
보다 깊은 개념이나 토론을 위한 미적분은 수학 관련 대학에 진학한 후에 해보도록 하죠.
결론부터 말하자면 미분은 접선의 기울기입니다.
저 내용을 알기 위해서는
함수, 일차함수, 이차함수, 점과 좌표, 기울기, 함수의 연속, 함수의 극한을 충분히 이해하고 있어야 합니다.
(혹시 부족한 부분이 있다면 복습을 하고 오는 편이 좋겠습니다.)
이 단원에서 알아야 하는 용어는 다음과 같습니다.
증분, 평균변화율, 순간변화율, 미분계수, 미분, 도함수.
증분은 증가량입니다. 점(2,3)에서 점(4,8)까지
x의 증분은 2, y의 증분은 5입니다. (중학교 때 이미 배웠겠죠.)
증분은 기호로 Δx 와 같이 나타냅니다. (삼각형 모양의 기호는 델타라고 읽습니다. 델타 x)
평균변화율은 다음과 같이 정의합니다.
중학교 1학년 과정의 일차함수에서 기울기랑 거의 같다고 생각하셔도 되겠습니다.
곡선에서도 구할 수 있기 때문에 기울기와 조금 다르지만요.

평균변화율을 완벽하게! 완벽하게 이해해야만 미분계수를 이해하기가 좋습니다.
다음의 용어를 여러 번 익혀 숙지하시기 바랍니다. (매우 중요!!!)
미분계수=순간변화율≒도함수=접선의 방정식=미분 (5가지)
귀찮으면 그냥 같다고 생각하셔도 됩니다. (희망=꿈=목표=바램=... 이런겁니다.)
다음의 기호를 여러 번 숙지하여 익히시기 바랍니다.

미분계수는 글로 설명하는 것이 쉽지 않습니다.
평균변화율 중 다음 식으로 이해하는 것이 그나마 쉽긴 합니다.
이 식은 (a, f(a))라는 점에서 x축 방향으로 Δx만큼 떨어진 (a+Δx, f(a+Δa))라는 점까지의 평균변화율(기울기)입니다.

여기서 Δx를 0에 가깝게 만들면 (a, f(a))에 접하는 접선의 기울기를 구할 수 있는데,
그게 바로 x=a에서 순간변화율, f'(a), x=a에서 미분계수입니다.
이해가 잘 안 간다면 영상을 찾아보거나 선생님께 질문합시다!
중요한 부분이기 때문에(미분의 첫 단추) 정확히 알고 넘어가야 합니다.
미분가능성과 연속성!
미분은 접선의 기울기이기 때문에 함수가 끊어진(불연속인) 곳에서는 구할 수 없습니다.
극한값: 좌극한과 우극한이 같아야 존재!
연속: 극한값과 함숫값이 같야 연속!
미분가능: 연속이고 부드러운 곡선이어야 미분가능!
예를 들어 함수 f(x)=|x-1|에서 x=1일 때, 함수가 꺾이기 때문에 부드럽지 않아요.
따라서, x=1에서 미분이 불가능합니다. (미분가능하지 않다.)
도함수는 뭘까요?
도함수는 영어로 derivative 라고 합니다. derivative는 유도하다 이끌다 이런 뜻입니다.
도함수는 한자로 導函數라고 합니다. 導는 이끌다 라는 뜻입니다.
도함수는 원래함수로부터 이끌려나온, 유도된 함수인거죠.
원래 함수의 모든 점에서 접선의 기울기 값을 함숫값으로 만든 함수입니다.
이걸 그림으로 보여주면 참 좋을텐데...
다시 한 번 강조합니다. 아래 두 줄은 꼭! 꼭! 명심해야 합니다!!!
미분계수=순간변화율≒도함수=접선의 방정식=미분 (5가지)

미분법은 f(x)에서 f'(x)를 구하는 것을 말합니다.
원래는 도함수의 정의를 이용해서 직접 구해보는 게 좋은데, 글로는 표현이 어렵네요.
다항함수를 미분했는데 왜 아래식이 나오는 지 궁금하다면 영사을 찾아보거나 선생님께 물어봅시다.
(대부분의 학교에서는 증명을 해줍니다.)

미분은 실수배와 덧셈, 뺄셈이 가능합니다. (곱셈과 나눗셈은 안됩니다.)

미분에서 곱셈은
곱의 미분법을 이용합니다.
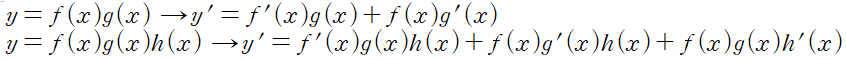
미분에서 나눗셈은 몫의 미분법을 이용하는데, '미적분'이라는 책에서 배웁니다.
따라서, 미적분을 선택하지 않는 학생은 배울 일이 없는거죠.
드디어 미분의 개념을 만들었습니다. 짝짝짝!
이제 미분법을 연습하고, 도함수를 활용하여 접선의 방정식도 구하고, 극댓값과 극솟값도 구할 수 있겠네요.
https://www.youtube.com/Vz3USX2SDfk
'수학 > 수학2' 카테고리의 다른 글
| [고2/고3 수학2] 6. 도함수의 활용(3) - 방정식, 부등식에의 활용, 속도, 가속도 (0) | 2021.07.21 |
|---|---|
| [고2/고3 수학2] 5. 도함수의 활용(2) - 증가, 감소, 극대, 극소 (0) | 2021.07.21 |
| [고2/고3 수학2] 4. 도함수의 활용(1) 접선의 방정식 (0) | 2021.07.15 |
| [고2/고3 수학2] 2. 함수의 연속 (0) | 2021.07.15 |
| [고2/고3 수학2] 1. 함수의 극한 (feat. 수학2 개론) (0) | 2021.07.15 |




댓글