
도함수의 활용(3)의 내용은 3가지입니다.
1. 삼차, 사차, ... 방정식의 근의 개수를 판별합니다.
2. 삼차, 사차, ... 부등식이 항상 성립함을 보이거나 미정계수의 범위를 구합니다.
3. 도함수와 속도, 가속도의 관계를 알아봅니다.
이차방정식의 근의 개수는 판별식이라는 훌륭한 식으로 한 번에 알아볼 수 있었습니다.
근을 구하지 않고도 확인할 수 있었습니다.
삼차 이상의 방정식에서 근을 구하지 않고 근의 개수를 구하는 방법으로
도함수를 활용합니다.
지난 시간 도함수의 활용(2)에서 그래프의 개형을 그리는 방법을 배웠는데요.
결론부터 말하자면,
그래프의 개형을 그리고 x축까지 그리면 되는 겁니다.
방정식 f(x)=0의 근은 함수y=f(x)의 x절편과 같기 때문이죠.
예제로 익히고 넘어갑시다.
삼차방정식 x3-6x2+2=0 의 서로 다른 실근의 개수를 구해봅니다.
f(x)=x3-6x2+2의 개형을 그리기 위해 미분합니다.
f'(x)=3x2-12x
3x2-12x=0 이 되는 x값을 구합니다.
x2-4x=0
x=0 또는 x=4
f(0)=2, f(4)=-30 이므로
x=0에서 극댓값 2, x=4에서 극솟값 -30을 갖게되고,
x축은 극댓값과 극솟값 사이에 있습니다.

정리해보면
극값을 갖는 삼차함수 f(x)에 대하여 삼차방정식 f(x)=0의 근은
극댓값, 극솟값이 모두 양수이거나 모두 음수 일 때 한 실근과 두 허근을 갖습니다.
극댓값, 극솟값 둘 중 하나가 0이면 한 실근과 중근(서로 다른 두 실근)을 갖습니다.
극댓값, 극솟값의 부호가 다르면 서로 다른 세 실근을 갖습니다.
부등식에서는 f(x)>0이 항상 성립함을 보이는 문제가 많습니다.
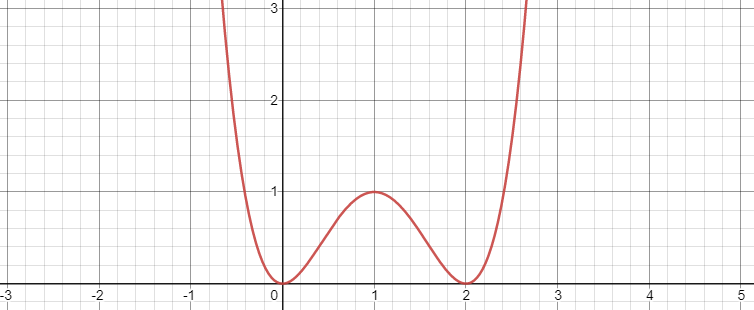
예를 들어 부등식 x4-4x3+4x2+k≥0 가 항상 성립하는 k의 범위를 구해보면
f(x)=x4-4x3+4x2+k
f'(x)=4x3-12x2+8x
4x3-12x2+8x=0
x3-3x2+2x=0
x(x-1)(x-2)=0
x=0 또는 x=1 또는 x=2
f(0)=k, f(1)=k+1, f(2)=k
따라서 x=0과 x=2에서 극소, x=1에서 극대
극솟값이 최솟값이고 최솟값이 0보다 크거나 같으면 항상 성립하기 때문에
최솟값 k≥0 이 정답입니다.
f(x)>g(x)의 형태로 나왔다면,
f(x)-g(x)>0으로 고쳐서 증명합니다. f(x)-g(x)도 h(x)등으로 치환하여 푸는 것이 편리합니다.
h(x)=f(x)-g(x)
h(x)>0
속도와 가속도는 물리시간에 등가속도 운동을 제대로 배웠다면 매우 쉽습니다.
간단히 말해서
위치 미분하면 속도
속도 미분하면 가속도
끝입니다.
구구절절 설명하자면 시간당 위치의 변화량이 속도인데
순간속도는 시간변화량을 0으로 보내면 되니까...(생략)
예를 들어 위치 x=3t2+4t+1 이라면, t=2일 때 속도는 얼마인가?
위치(x)를 미분하면 속도 v=6t+4가 되고, t=2일 때 속도는 16이 됩니다.
위의 속도를 잘 이해했다면
시각에 대한 변화율을 미분으로 표현할 수 있습니다.
시각(t)에 대한 길이(ℓ)의 변화율은 ℓ을 시각(t)에 대해 미분해주면 됩니다. ℓ'
시각(t)에 대한 넓이(S)의 변화율은 S를 시각(t)에 대해 미분해주면 됩니다. S'
시각(t)에 대한 부피(V)의 변화율은 V를 시각(t)에 대해 미분해주면 됩니다. V'
예를 들어 시각 t에서의 반지름의 길이가 3t인 구에 대하여 t=2일 때 구의 겉넓이의 변화율을 구하면?
구의 겉넓이 S=4𝝅r2 에서 반지름(r)이 3t이므로
S=4𝝅(3t)2, S=36𝝅t2
S'=72𝝅t
t=2일 때
겉넓이의 변화율은 144𝝅가 됩니다.
도함수의 활용 (1), (2), (3)을 모두 배웠습니다.
핵심은 접선의 기울기가 미분이라는 것! (5가지 용어! 5가지 기호! 꼭 알아두세요!!)
다항함수(특히 삼차, 사차)의 그래프를 그리는 것!
이렇게 두 가지라 할 수 있습니다.
개념이 어느정도 잡혔다면 문제를 많이 풀어야 합니다.
문제가 잔뜩 수록된 문제집으로 마구마구 풀어주시기 바랍니다.
복습! 복습! 복습!
복습하면 복이옵니다.
'수학 > 수학2' 카테고리의 다른 글
| [고2/고3 수학2] 8. 정적분 (0) | 2021.07.25 |
|---|---|
| [고2/고3 수학2] 7. 부정적분 (0) | 2021.07.21 |
| [고2/고3 수학2] 5. 도함수의 활용(2) - 증가, 감소, 극대, 극소 (0) | 2021.07.21 |
| [고2/고3 수학2] 4. 도함수의 활용(1) 접선의 방정식 (0) | 2021.07.15 |
| [고2/고3 수학2] 3. 미분계수와 도함수 (0) | 2021.07.15 |




댓글