
수학은 수나 양을 계산하는 것을 기본으로 하고 있지만,
논리 또한 중요하게 다루고 있습니다.
논리학의 기본이 되는 명제에 대해서 공부해보도록 하겠습니다.
명제는 참, 거짓을 분명하게 구분할 수 있는 문장이나 식을 말합니다.
예를 들어 '멋진지니는 잘생겼다.'라는 문장은 사실일 수도 있지만,
분명하게 구분할 수 있는 기준이 없기 때문에 참 또는 거짓이라 할 수 없고
명제가 아닙니다.
명제라는 단원에서는 다음 용어에 대한 이해가 필요합니다.
명제, 정의, 증명, 정리,
조건, 진리집합, 부정, 가정, 결론, 반례,
역, 이, 대우,
필요조건, 충분조건,
이미 알고 있다면 명제라는 단원의 문제를 해결하는 데 크게 무리가 없을 것입니다.
용어에 대한 이해!! 확실하게 해 두어야 하는 단원입니다.
명제는 참 또는 거짓을 분명하게 구분할 수 있는 문장이나 식입니다.
정의는 용어의 뜻! 원래 그런겁니다. 토달면 안됩니다. (호기심을 가질 수는 있죠.)
증명은 참임을 밝히는 것! 정의 또는 이미 옳다고 알려진 성질을 이용하여 어떤 명제가 참이라는 걸 보이는 겁니다.
정리는 성질! 이미 참이라고 증명된 명제 중 기본이 되는 것이죠.
예를들어
'이등변 삼각형은 두 변의 길이가 같다.'는 정의!
'이등변 삼각형의 두 밑각의 크기는 같다.'는 정리!입니다.
증명하는 과정은 중학교 2학년 2학기 과정에 있으니 찾아보셔도 좋을 것 같습니다.
조건은 간단히 말하자면 가정이나 결론 같은 것인데,
정확하게 말하면 문자를 포함한 식에서 문자의 값에따라 참 거짓이 정해질 때의 식 또는 문장을 조건이라 합니다.
(정확하게 말하면 어렵죠? 간단하게 가정, 결론 이런거 통틀어서 조건!)
가정과 결론은 'p이면 q이다'라는 명제에서 p를 가정, q를 결론이라 합니다.
기호로 p→q로 나타냅니다.
진리집합은 조건을 집합으로 나타낸 것이고요.
부정은 조건 p에 대하여 'p가 아니다'를 부정이라 합니다.
기호로 ~p로 나타냅니다.
예를들어 'x가 4의 배수이면 x는 짝수이다'라는 명제에서
조건: x가 4의 배수, x는 짝수
가정: x가 4의 배수
결론: x는 짝수
가정의 부정: x는 4의 배수가 아니다
결론의 부정: x는 짝수가 아니다 (또는 x는 홀수이다)
가정의 진리집합: {4, 8, 12, ...}
결론의 진리집합: {2, 4, 6, ...}
이런겁니다.
반례란 명제가 거짓인 경우에는 거짓임을보이는 방법입니다.
p이면 q이다가 거짓임을 보이려면 p이지만 q가 아닌 것을 보여주면 되겠죠.
예를들어 '저 동물이 새라면 저 동물은 날 수 있다'라는 명제는 거짓입니다.
반례로 '닭'을 들어주면 되겠죠. 닭은 새이지만 날 수는 없으니까요.
명제의 기본적인 용어는 정리가 되었습니다.
이번에는 조금 더 깊이 알아보도록 하겠습니다.
'p이면 q이다'를 명제라고 하는데요.
이 명제의 역, 이, 대우를 살펴봅시다.
역은 가정과 결론을 바꾼 명제,
대우는 가정과 결론을 각각 부정하고 바꾼명제를 말합니다.
현(2021기준) 교육과정에서는 명제의 역과 대우만 배우도록 되어있지만 '이'라는 것도 있습니다.
이는 가정과 결론을 각각 부정한 명제입니다.
명제: p이면 q이다.
역: q이면 p이다.
대우: ~q이면 ~p이다.
이: ~p이면 ~q이다.
(예전 교육과정에서는 명제의 역, 이, 대우를 배웠죠)
여기서 중요한 것은
명제 (p→q)가 참이면 대우(~q→~p)가 참이다.
라는 것입니다.
예를 들어 '나는 키가 180cm이하이다.' 라는 명제가 참이라면
대우인 키가 '180cm초과이면 내가 아니다.'도 역시 참입니다.
명제의 대우가 항상 참인 것을 이용하여 증명하는 방법을 대우법이라고 합니다.
또는, 그리고, 모든, 어떤?
조건에서 '또는'의 부정은 '그리고'가 됩니다. '그리고'의 부정은 '또는' 이겠죠.
예를 들어 '2는 소수이고 홀수이다.'를 부정해보면 '2는 소수가 아니거나 짝수다'가 됩니다.
명제는 집합과 밀접한 관계를 갖고 있습니다.
'부정'은 여집합
'그리고'는 합집합
'또는'은 교집합에 해당됩니다.
집합에서 드모르간의 법칙이 중요하다고 강조드린 적이 있는데요.
다음 식을 명제로 표현해봅시다.

'A또는B이다'의 부정은 'A가 아니고 B도 아니다'가 되는겁니다.
또한, 명제에서 '모든'의 부정은 '어떤', '어떤'의 부정은 '모든'입니다.
알고 넘어갑시다.
필요조건과 충분조건을 살펴보겠습니다.
명제 'p이면 q이다'가 참일 때, 기호로 다음과 같이 나타냅니다.

여기서 p는 q이기 위한 충분조건이라하고, q는 p이기 위한 필요조건이라고 합니다.
p는 q가 되기에 충분하기 때문에 충분조건이고
q는 p를 필요로 하기 때문에 필요조건이라는건데,
너무 헷갈리고 암기하기가 어렵습니다.
미국에서는 암기하기 쉽도록 4방위 기호를 90도 회전시켜서 화살표 모양을 만든 후
Sufficient condition(충분조건)과 Necessary condition(필요조건)의 앞글자를
South와 North에 대응시켜 암기합니다.

우린 한국사람이니까
화살이 출발하는 쪽이 충분조건
화살이 도착하는 쪽은피나니까 필요조건
이라고 암기합시다.
'p이면 q이다.'와 'q이면 p이다.'가 모두 참일 때, 다음과 같이 나타내고
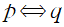
p는 q의 필요충분조건, q는 p의 필요충분조건이라 합니다.
진리집합과의 관계도 중요합니다.
가정 p의 진리집합 P가 결론 q의 진리집합 Q의 부분집합일 때, P는 충분조건, Q는 필요조건이 됩니다.
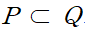
끝으로 여러 가지 증명법을 살펴봅시다.
명제가 참인 경우에는 증명을 해야 합니다. (정의는 증명할 필요가 없겠죠!)
증명법에는 크게 직접증명법과 간접증명법이 있습니다.
직접증명법은 연역증명을 말하는데, 쉽게 이야기하면 삼단논법! A=B, B=C 이면 A=C
간접증명법에는 여러 가지가 있지만,
고등학교 수학시간이니까 세 가지만 알아둡시다.
대우법, 귀류법, 수학적 귀납법(고2 과정입니다).
대우법은 조금 전에 본 방법입니다.
'명제가 참이면 대우가 참이다.'를 이용하여 증명하는 겁니다.
예를 들어 'x제곱이 4가 아니면 x는 2가 아니다.'는 알아보기에 조금 불편할 수 있습니다.
따라서, 대우를 사용하면 'x=2이면 x제곱=4이다.'가 되기 때문에 참이 되는 것을 금방 알 수 있습니다.
귀류법은 선생님께 설명을 직접 들어도 이해가 어려울 수 있습니다.
글로 설명하려니 더더욱 이해가 안 갈 것 같지만, 최선을 다해보도록 하겠습니다.
아래 문장을 여러 번, 빠르게! 빠르게 읽어서 자신의 것으로 만드세요. (5번 정도 읽어보세요.)
'결론을 부정하여 가정에 모순이 생김을 보이는 방법.'
이게 귀류법인데 무슨 말인지 알아듣기 어렵지 않나요?
예를 들어 '호랑이는 육식동물이다.'를 귀류법으로 증명하려면
결론 부정: 호랑이가 육식동물이 아니라면 (여기서 쓸데 없는 생각 하시면 안됩니다. 이상한 토달지 마시고)
가정에 모순: 초식동물이라서 풀을 먹어야 하는데..., 호랑이는 풀을 안먹죠!
가정에 모순이 생김을 보였으므로 결론을 부정할 수 없습니다.
그래서 명제가 참입니다.
집합과 명제는 생소한 용어들이 많이 나오기 때문에 적응하는 데 시간이 필요합니다.
시간을 두고 꾸준히 연습해야 좋은 결과를 얻을 수 있습니다.
'수학 > 고1수학(하)' 카테고리의 다른 글
| [고1 고등수학하] 5. 유리식과 유리함수 (1)유리식 (feat. 번분수 초간단) (0) | 2021.08.02 |
|---|---|
| [고1 고등수학하] 4. 함수 (0) | 2021.07.20 |
| [고1 고등수학하] 3. 명제_2 절대부등식 (0) | 2021.07.14 |
| [고1 고등수학하] 2. 집합의 연산 (0) | 2021.07.14 |
| [고1 고등수학하] 1. 집합의 뜻과 표현 (2) | 2021.07.14 |




댓글