
지난 단원인
유리식(링크)과 비례식(링크)에 대해 충분히 이해를 했다면,
유리함수를 배우기 좋습니다.
(이해가 안됐다면 어려운;;)
유리함수가 뭔가요?
유리함수는
y=f(x)=(유리식)일 때, 유리함수라 합니다.
f(x)가 다항식이라면 다항함수가 되는데,
다항함수도 유리함수에 포함됩니다.
여기서 주로 배우게 되는 것은
유리함수라기보다는 분수함수입니다.
단원은 유리함수인데,
유리식(링크)은 배웠으니, 함수만 배우면 되겠네요.
함수! 이것만 알면 끝!
함수에서 자주 등장하는 내용들을 미리 알고 있어야 합니다.
정의역, 공역, 치역, 그래프 그리기,
점(p, q)이 함수 y=f(x)를 지날 때, 대입하기,
함수와 함수가 만날 때, 연립하기,
두 함수의 교점의 x좌표는 연립방정식의 해,
역함수, 합성함수 구하기, 평행이동하기,
x축대칭, y축대칭, 원점대칭, y=x대칭 구하기,
이정도만 알고 있으면 함수는 걱정 없습니다.
일차함수에서 가장 중요한 것은?
기울기
이차함수에서 가장 중요한 것은?
꼭짓점
유리함수에서 가장 중요한 것은?
점근선
유리함수를 그려봅시다.
y=1/x는 빨간색, y=-1/x는 초록색입니다.
여기서 x축 방향으로 한없이 가더라도 그래프는 0이 되지 않는데,
x축을 점근선이라 합니다. x축은 방정식으로 y=0으로 쓰죠.
y축도 마찬가지! 점근선이 됩니다. y축은 방정식으로 x=0으로 씁니다.
평행이동을 시켜봅시다.
x축방향으로 1만큼, y축방향으로 2만큼 평행이동 시키면
다음 그림과 같아집니다.
이때 점근선은 x=1(아까 y축에 해당되었던 부분)
y=2(아까 x축에 해당되었던 부분)
이렇게 되겠죠.

함수는 그래프가 중요하기 때문에
글로 설명하기에는 어려움이 좀 있네요.
저는 교과서나 개념서가 아니기 때문에
시험에 주로 출제되는 유형에 대해서만 언급하겠습니다.
유리함수에서는 정의역, 치역을 묻거나
점근선을 묻거나
평행이동한 함수를 구하거나
역함수를 구하거나
유리함수를 대칭이 되도록하는 직선을 구합니다.
다음 함수에 대해 분석을 해봅시다.
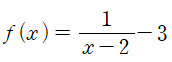
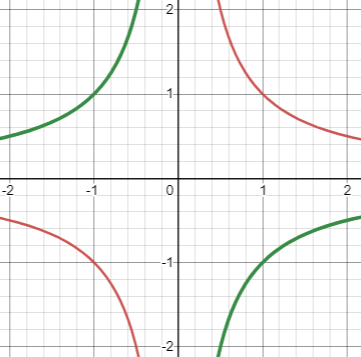
f(x)=1/x의 함수를 x축방향으로 2만큼, y축방향으로 -3만큼 평행이동한 함수입니다.
정의역은 {x|x≠2인 모든 실수}, 치역은 {y|y≠-3인 모든 실수}
점근선은 x=2, y=-3입니다.
역함수를 구하는 식은 다음과 같습니다.

유리함수를 대칭이 되도록 하는 직선의 방정식을 구해봅시다.
유리함수는 x축과 y축에 각각 평행한 직선을 점근선으로 갖는
수직 쌍곡선이기 때문에
점근선의 교점을 지나고
기울기가 1인 직선과, 기울기가 -1인 직선에 대칭이 됩니다.
위의 유리함수는
점근선의 교점이 (2, -3)이므로
y=x-5와 y=-x-1의 두 직선에 대칭이 됩니다.
함수, 특히 함수의 그래프는 글로 이해하기에는 조금 어려울 수 있습니다.
좋은 선생님이나 좋은 영상을 찾아서 설명을 듣도록 해봅시다.
'수학 > 고1수학(하)' 카테고리의 다른 글
| [고1 고등수학하] 7. 경우의 수(순열과 조합) (feat. 확률과 통계 개론) (0) | 2021.08.06 |
|---|---|
| [고1 고등수학하] 6. 무리식과 무리함수 (0) | 2021.08.05 |
| [고1 고등수학하] 5. 유리식과 유리함수 (2) 비례식 (0) | 2021.08.03 |
| [고1 고등수학하] 5. 유리식과 유리함수 (1)유리식 (feat. 번분수 초간단) (0) | 2021.08.02 |
| [고1 고등수학하] 4. 함수 (0) | 2021.07.20 |




댓글